In meinem ersten Posting, welches mehr Inhalt hat, als einen dummen QR-Code-Witz, möchte ich mich einem kleinen Kniff widmen, der mir gerade mal wieder aufgefallen ist, als ich ein paar Aufwärmübungen im Java-Programmieren machte, um wieder etwas in die Syntax einzusteigen.

Es passiert so oft: Man schreibt ein schönes, performantes Program, im schlimmsten Fall sogar eines, das mit Computergrafik zu tun hat und weigert sich aus unbekannten Gründen, für trigonometrische Funktionen Look-Up-Tables zu verwenden. Nun berechnet man also vllt. einige tausend Male in wenigen Sekunden in seinem Programm z.B. den Cosinus einer reellen Zahl.

Dabei wird man rasch feststellen, dass die Java-interne Funktion "Math.cos(double x)" zwar relativ schnell ist, aber man doch gern noch ein wenig schneller wäre.

Dazu überlegt sich der findige Mathematiker in uns wohl recht schnell, dass er ja eine Annäherungsfunktion an den Cosinus besser selbst implementieren möchte, z.B. die bekannte Reihe:

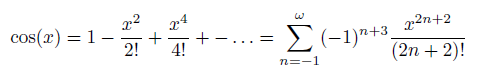
Die Summe ist recht schnell in Code umgesetzt und resultiert in der Methode


final static double EPS = 1E-12; //gewünschte Genauigkeit
public static double faculty(long x); //Fakultätsfunktion
public static double slowCos(double x){
double part;
float sum = 0;
int n = -1;
do{
part = Math.pow(-1, n+3) * (Math.pow(x,2*n+2)/faculty(2*n+2));
sum += part;
n++;
} while (Math.abs(part) > EPS);
return sum;

 

Ärgerlicher Weise ist diese Art den Cosinus anzunähern noch langsamer, als die Java-interne Methode...also überlegt man sich fix, wie man diesem Problem aus dem Weg gehen könnte. Nach einiger Denkzeit kommt man dann auf die rettende Idee: "Warum programmiere ich eigtl. haarklein das Summenzeichen nach und nicht die Summe, die davor steht!"


final static double EPS = 1E-12; //gewünschte Genauigkeit
public static double fastCos(float x){
double sum = 1;
double part = 1;
double xx = x*x; //vorberechnetes x² für noch mehr Geschwindigkeit!
int n = 2;
do{
part = part * -1;
part = part * xx;
part = part / ((n-1)*n);
sum += part;
n += 2;
} while (Math.abs(part) > EPS);
return sum;
}
Siehe da! Alle aufwändigen Komponenten der Schleife, wie Potenzen und Fakultät wurden aufgelöst und in der Schleife werden nur noch triviale (und vor allem schnelle!) Additionen und Multiplikationen ausgeführt!

Beim Ausprobieren stellt man fest, es fühlt sich schneller an, daher hier zum Vergleich über 1000 Versuche gemittelte Geschwindigkeiten der verschiedenen Algorithmen bei einer Genauigkeit auf "1E-12" also 12 Stellen hinter dem Komma:

AlgorithmusDurchschnittsdauer/Berechnung

slowCos	0.1023 ms
fastCos	0.0051 ms
Math.cos	0.0191 ms

Der fastCos-Algorithmus ist also (auf meinem System) im Schnitt ca. 4x so schnell, wie der in Java6 integrierte Math.cos Befehl. Die Lektion die daraus hervorgeht sollte sein: Auch gegebene, vorimplementierte Funktionen können Schwächen in Sachen Geschwindigkeit und sogar Genauigkeit aufweisen! Zum Testen sind diese Funktionen in aller Regel super, bzw. für kleinere Projekte. Sollte es an Echtzeitkritischere Dinge gehen, empfiehlt es sich stets, sich auch über solche Kleinigkeiten mal Gedanken zu machen, da allzuoft genau solche Kleinigkeiten zu gigantischen Performanz-Einbußen in Endanwendungen sorgen.

 

Damit verabschiede ich mich auch erstmal und wünsche eine schöne Zeit!

Euer André